Stream

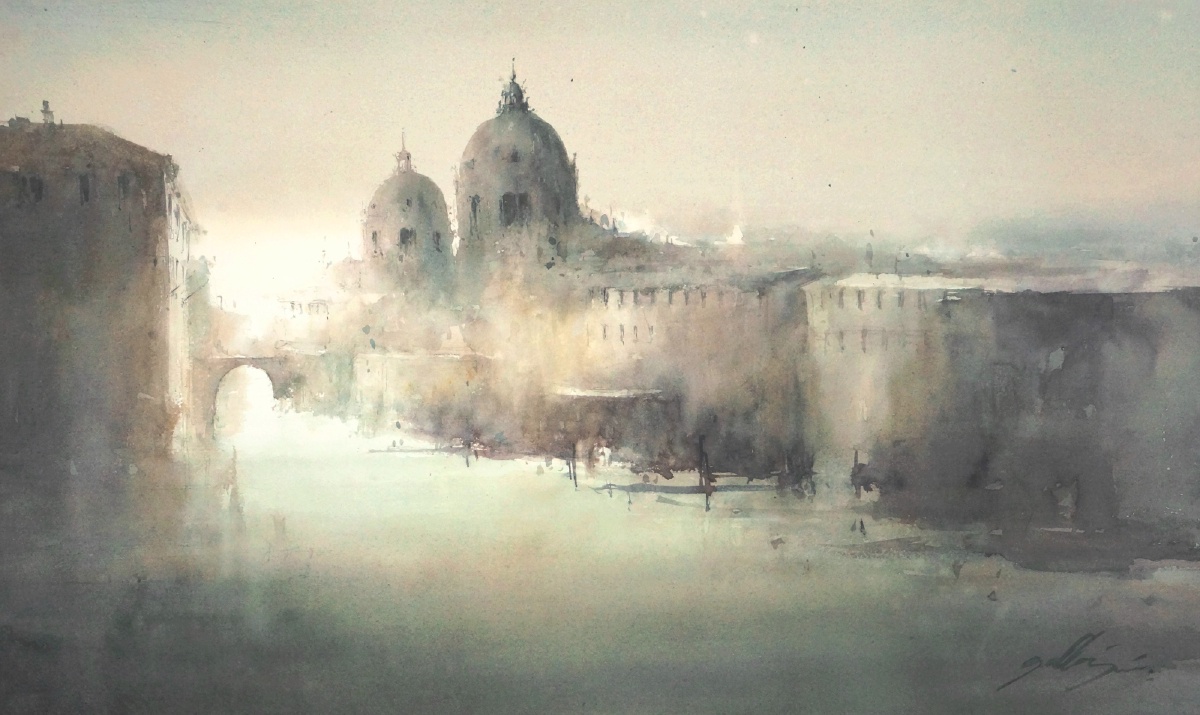
A professional artist, international judge, teacher, organiser of international exhibitions, artistic director of the magazine The Art of Watercolour and personal adviser to artists and art societies, Janine has won numerous awards for her paintings and gained a reputation as an artist, offering her help, knowledge and advice to others.

Having lived on three continents, in 5 countries, in contact with thousands of artists from all over the world, she now wishes to share her experience with as many people as possible, with the aim of creating an inspiring, stimulating and effective environment for all those who want to make progress with their painting.

The sudden high temperatures not only cause the bright glow along the dramatic streak but also melt and vaporize the meteor's component rock and ice, creating dust. Wind in the atmosphere typically blows this dust away over the next few seconds, leaving no visible trace after only a few minutes. Much of this dust will eventually settle down to the Earth. The featured image was captured in mid-December, coincident with the Geminids meteor shower. On the upper left is Sirius, the brightest star in the night sky, while in the foreground is fog-engulfed Huangshan, the Yellow Mountains of eastern China..